どもどもっ、さくですよ!
今回も授業で問われる「隣りの領域と色を被らず塗り分けるのに必要な色の数」の正解を記事にしたいと思います。
えー、この問題はよく分からなかったので自力で正解しました(´-ω-`)
時間がある人は、私みたいに紙に図形を書いてみましょう。
意外と簡単に解けますよヾ(〃^∇^)ノ
数学の宇佐美からの問題
ではでは、早速本題に入ります。
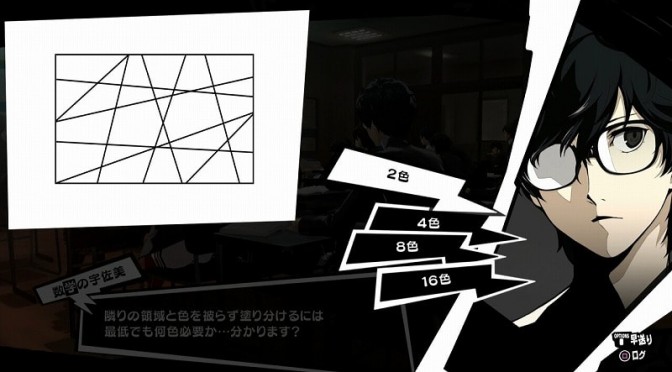
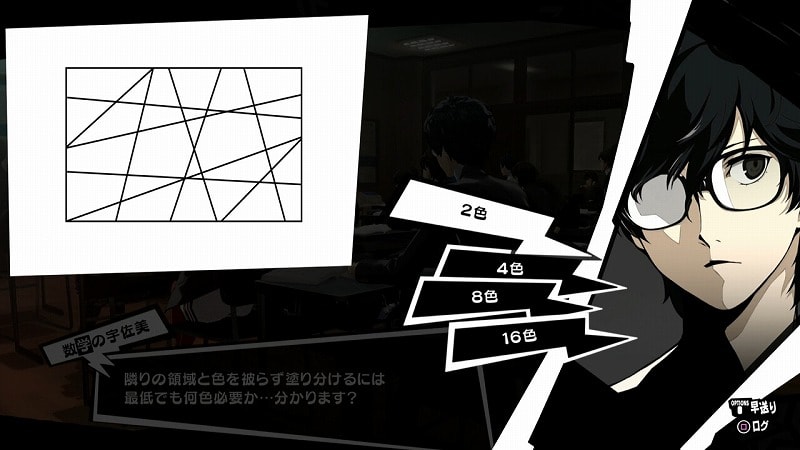
「隣りの領域と色を被らず塗り分けるには最低でも何色必要か…分かります?」
ごめんなさい分からないです!
むしろ、最初何言ってるか全然分からなかった\(^o^)/
この問題は4択です。
「2色」「4色」「8色」「16色」。
分からない人は、私みたいに実際の紙に書いてみましょう。
やってみると意外と簡単に分かりますよーヾ(〃^∇^)ノ
正解
というわけで正解は「4色」でした!
おぉ、たまたま正解してしまったw
これはラッキー(●´艸`)
どうやら「4色定理」という法則があるらしく、平面図なら4色あれば塗り分けられるそうです。
へ、へぇーそうなんだ(棒読み
そんなの知らないし始めて聞いたし!!!
最後に
以上で、「隣りの領域と色を被らず塗り分けるのに必要な色の数」の正解を終わります。
「4色定理」…これまた勉強になりましたね!
せっかく素晴らしいことを教えてもらったので、いつか現実でも使ってやりましょう(ぇ





















コメント
4色定理とか初めて聞きましたわー
ニッポンノコトバトテモムズカシネー
4色定理の証明?とかゆーのを興味本位でGoogleセンセに聞いてみましたが、何仰ってるかちんぷんかんぷんですたわ(°∀°)アヒャヒャヒャヒャヒャヒャヒャヒャヒャヒゴッ!!!ゴホッ!ゴホッオエェェェー!!!
……あー、早くペルソナ届かないかなぁ( = =) トオイメ
>だめぼんさん
基本的に問題難しいですよねw
って、まだペルソナ5届いてないんかーぃ\(^o^)/